A Estrutura Espectral dos Primos
Uma base matemática estável para um mundo instável.
A CIP é fundamentada na função diferencial dos primos, $\Delta\pi(x)$, que revela a assimetria persistente entre os primos estruturadores (que definem a estrutura passada) e os estabilizadores (que equilibram o presente). As visualizações abaixo demonstram os princípios que sustentam a Matriz Harmônica.
Gráfico 1: A Dualidade Primal em Ação
A contagem de primos estruturadores ($\pi(x/2)$) comparada com a de estabilizadores ($\pi(x) - \pi(x/2)$).
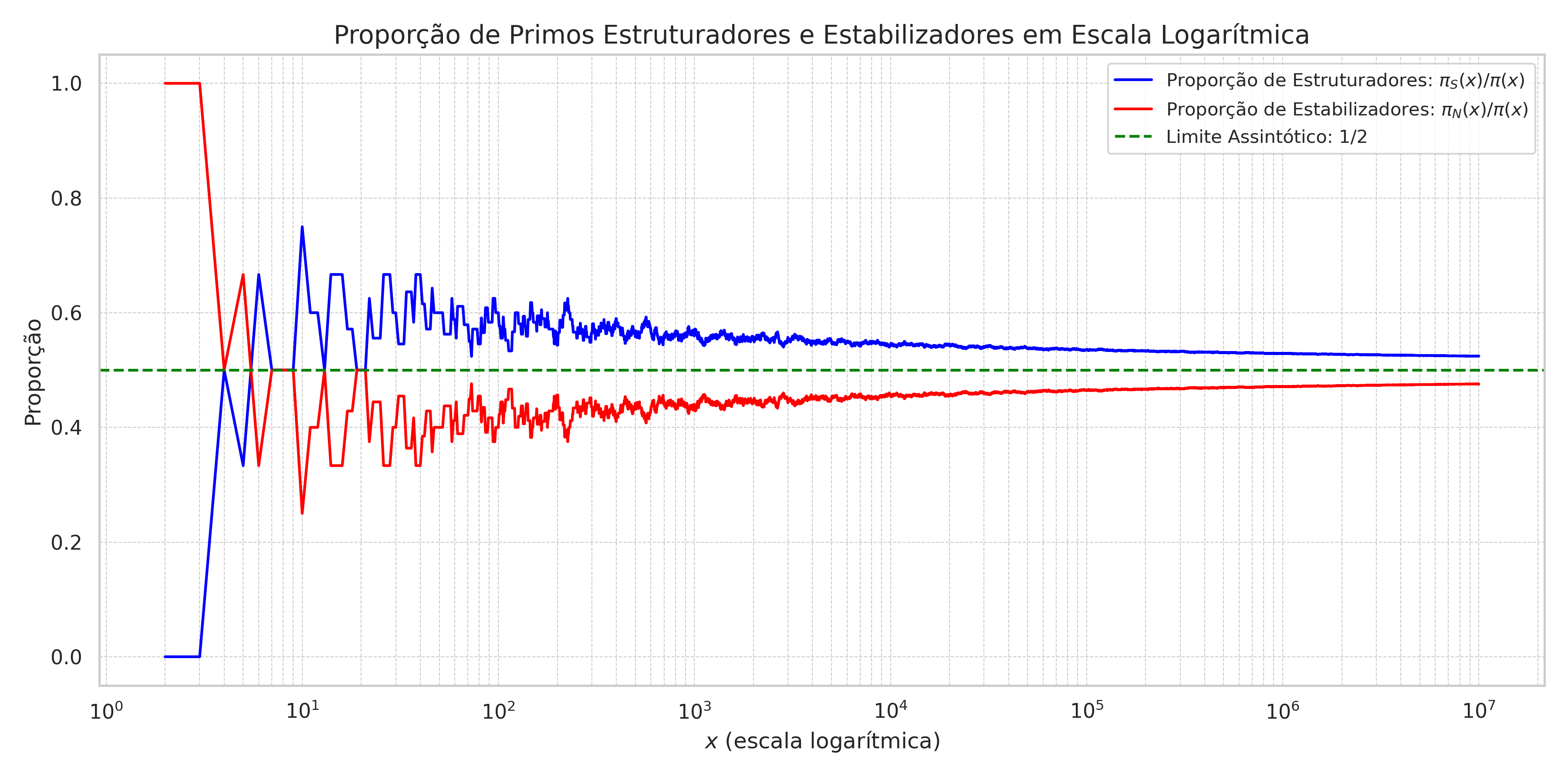
Gráfico 2: A Tendência de $\Delta\pi(x)$
O comportamento de $\Delta_\pi(x)$ muda com a escala. A função nasce numa oscilação dramática e, à medida que $x$ cresce, entra num mergulho contínuo em valores negativos. É a manifestação visual do "déficit de ordem" inerente à expansão do cosmos numérico.
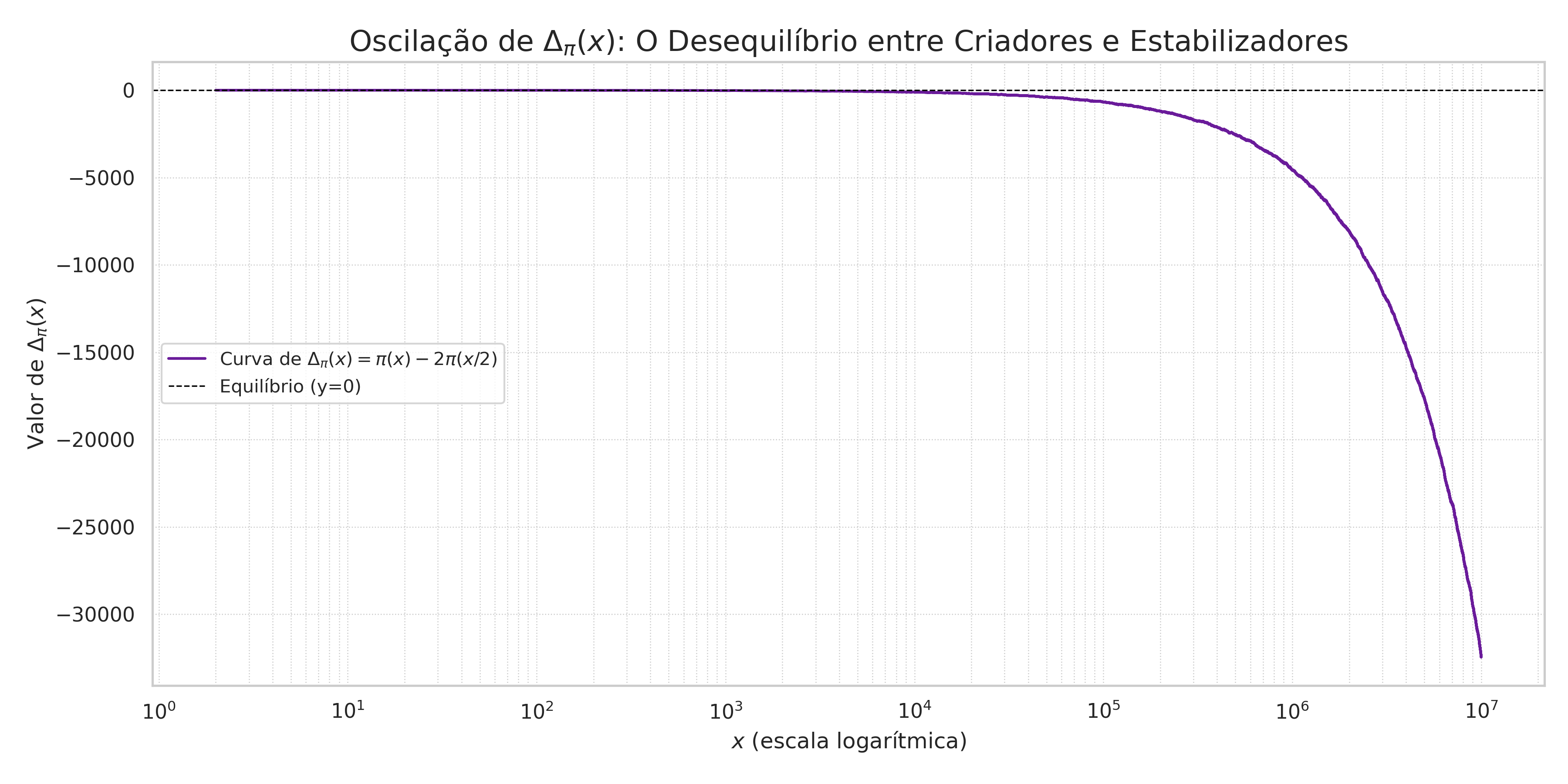
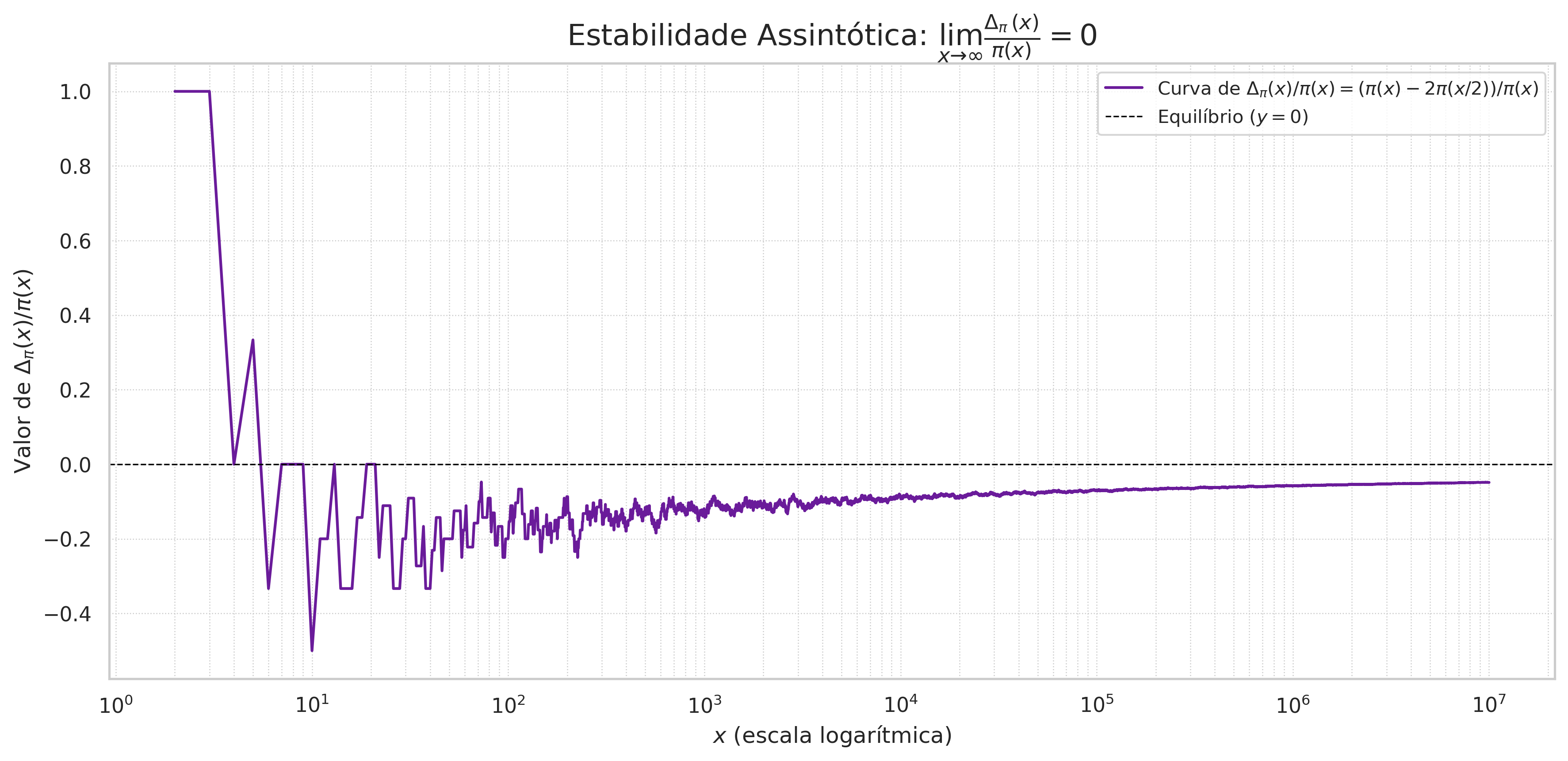
Gráfico 3: A Estabilidade Assintótica
Apesar do mergulho em valores absolutos, a influência relativa de $\Delta\pi(x)$ tende a zero. O sistema é assintoticamente estável, como mostra o limite:
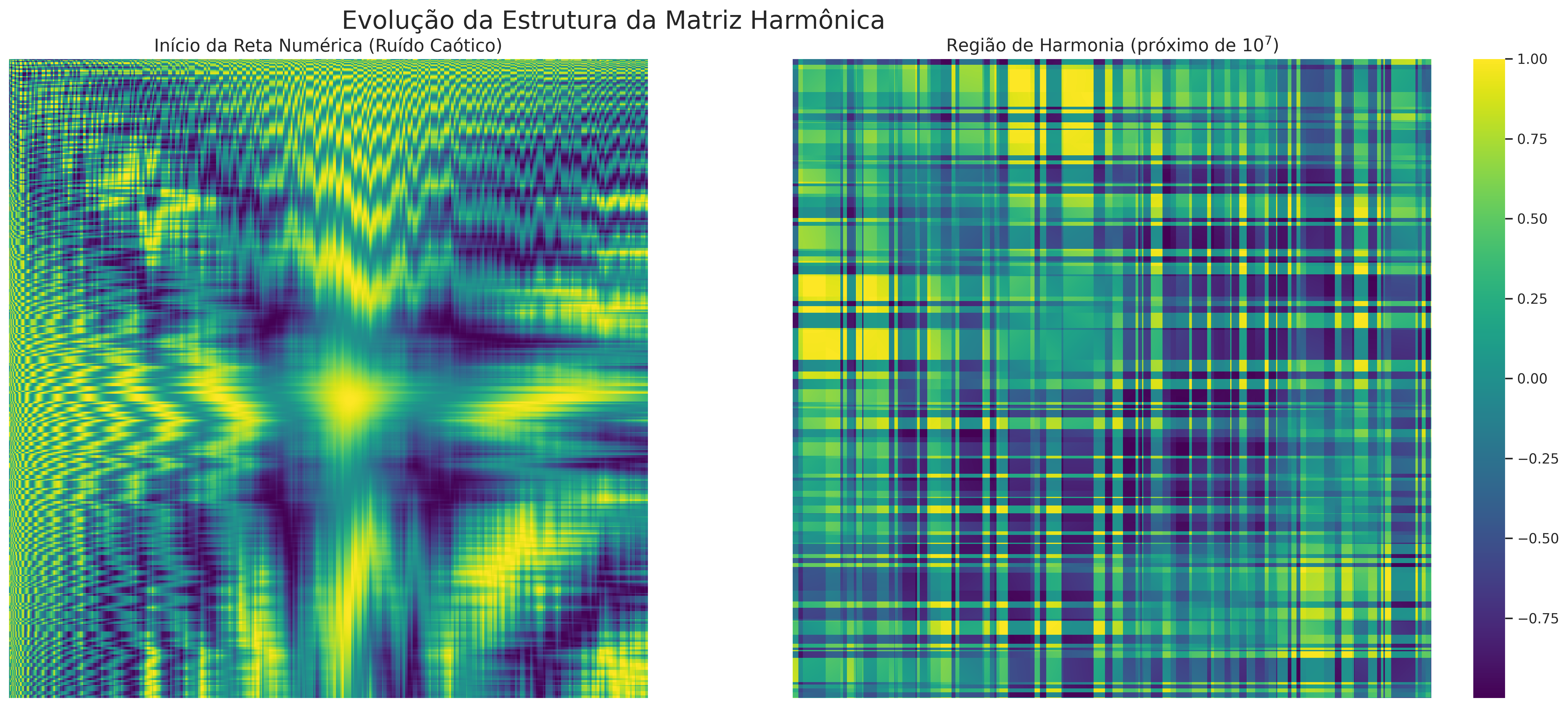
Esta estabilidade espectral, que emerge em regiões de alta harmonia (acima de $10^7$), é a âncora da CIP.
Gráfico 4: Do Caos à Harmonia
Os heatmaps da Matriz Harmônica em diferentes escalas demonstram visualmente a sua evolução: da turbulência dos primeiros inteiros à "tapeçaria" ordenada das projeções determinísticas.